FlashConv: Speeding up state space models

State space models (SSMs) are a promising alternative to attention – they scale nearly-linearly with sequence length instead of quadratic. However, SSMs often run slower than optimized implementations of attention out of the box, since they have low FLOP utilization on GPU. How can we make them run faster? In this blog post, we’ll go over FlashConv, our new technique for speeding up SSMs. We’ll see how in language modeling, this helped us train SSM-based language models (with almost no attention!) up to 2.7B parameters – and run inference 2.4x faster than Transformers.

In our blog post on Hazy Research, we talk about some of the algorithmic innovations that helped us train billion-parameter language models with SSMs for the first time.

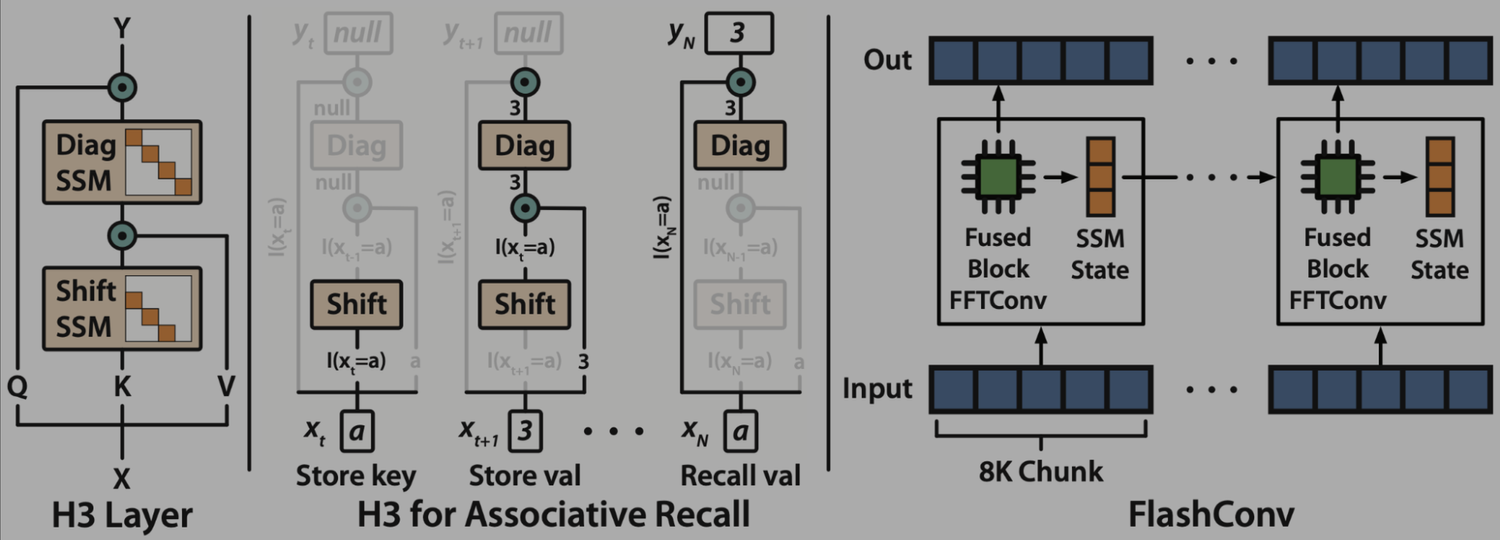
A Primer on State Space Models

State space models (SSMs) are a classic primitive from signal processing, and recent work from our colleagues at Stanford has shown that they are strong sequence models, with the ability to model long-range dependencies – they achieved state-of-the-art performance across benchmarks like LRA and on tasks like speech generation.

For the purposes of this blog post, there are a few important properties of SSMs to know:

• They generate a sequence length-long convolution during training
• They admit a recurrent formulation, which makes it possible to stop and restart the computation at any point in the convolution

The convolution dominates the computation time during training – so speeding it up is the key bottleneck.

FlashConv: Breaking the Bottleneck

So how do you efficiently compute a convolution that is as long as the input sequence (potentially thousands of tokens)?

FFT Convolution
The first step is using the convolution theorem. Naively, computing a convolution of length N over a sequence of length N takes $O(N^2)$ time. The convolution theorem says that we can compute it as a sequence of Fast Fourier Transforms (FFTs) instead. If you want to compute the convolution between a signal $u$ and a convolution kernel $k$, you can do it as follows:

$iFFT(FFT(u) \odot FFT(k)),$

where $\odot$ denotes pointwise multiplication. This takes the runtime from $O(N^2)$ to $O(N \log N)$.

‍

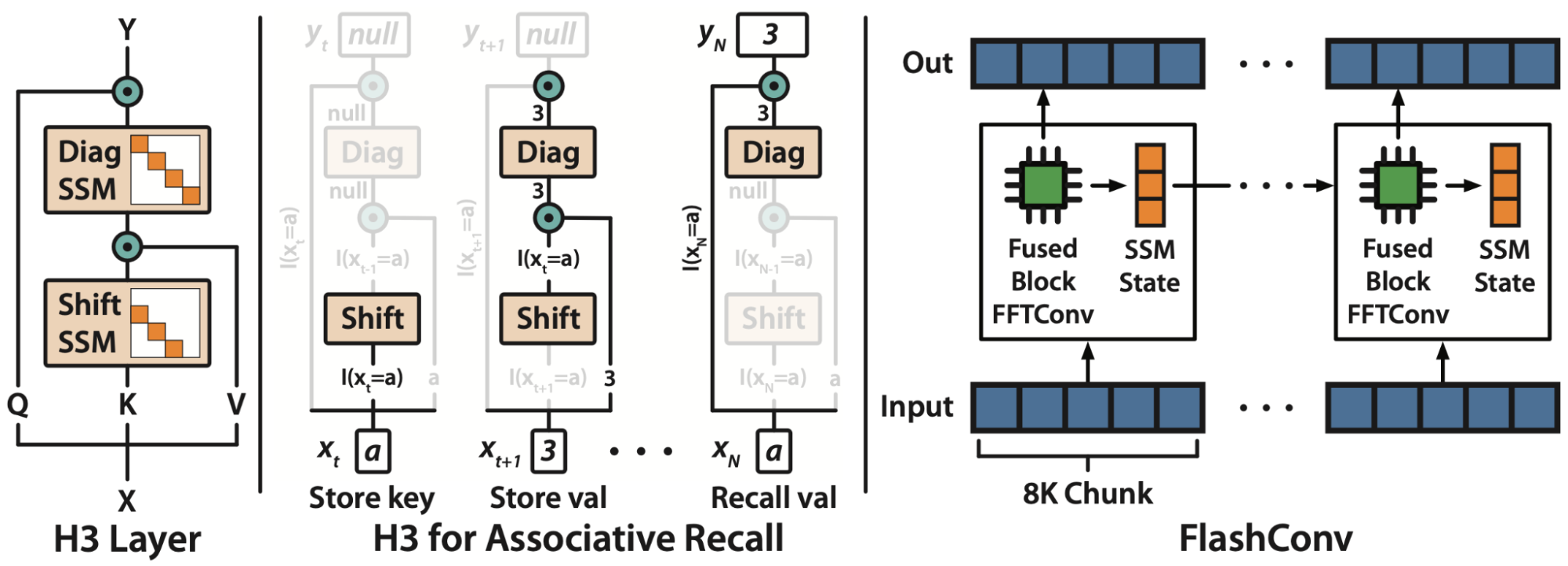
So we can just use torch.fft, and outperform attention:

Wait… the asymptotic performance looks good, but the FFT convolution is still slower than attention at sequence lengths <2K (which is where most models are trained). Can we make that part faster?

Fused FFT Convolution
Let’s look at what the PyTorch code actually looks like:

u_f = torch.fft.fft(u)
k_f = torch.fft.fft(k)
y_f = u_f * k_f
y = torch.fft.ifft(y_f)

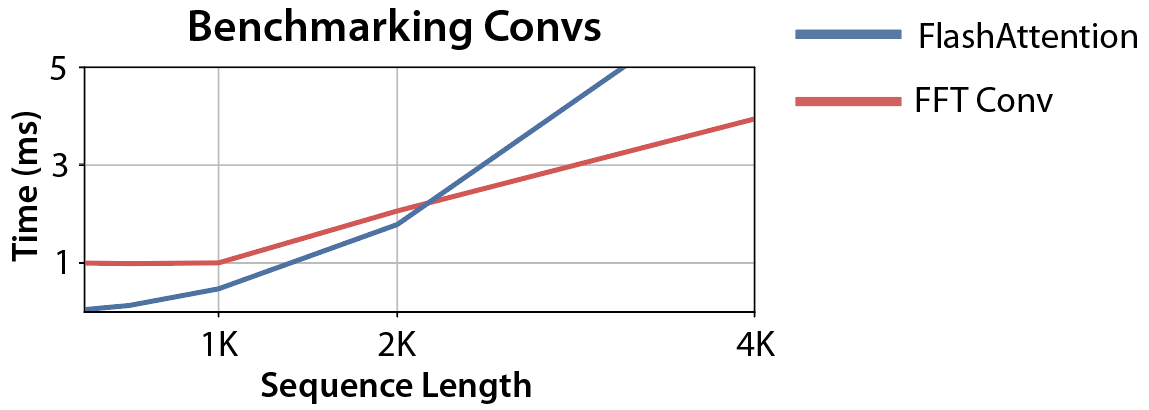
Each of those lines requires reading and writing $O(N)$ data to GPU HBM – which makes the entire operation I/O-bound. But we know how to solve this! We can write a custom CUDA kernel that fuses those operations together (and soon, PyTorch 2.0 might do it automatically):

‍

Progress! The crossover point is now 1K – good news for language models.

Block FFT Convolution
But can we do better? It turns out that now the operation is compute-bound.

Why? GPUs have fast specialized matrix multiplication units, such as tensor cores. Attention can take advantage of these, but standard FFT libraries cannot. Instead, they have to use the slower general-purpose hardware – which can be a significant gap in performance (on A100, tensor cores have 16x the FLOPs of general-purpose FP32 computations).

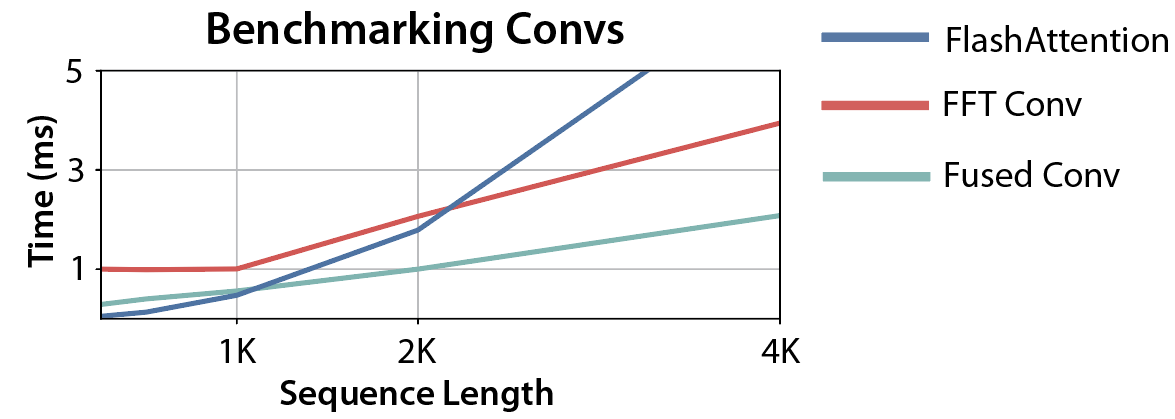
So we need some way to take advantage of the tensor cores on GPU. Luckily, there’s a classic algorithm called the Cooley-Tukey decomposition of the FFT, or six-step FFT algorithm. This decomposition lets us split the FFT into a series of small block-diagonal matrix multiplication operations, which can use the GPU tensor cores. There are more details in the paper, but this gives us more performance again!

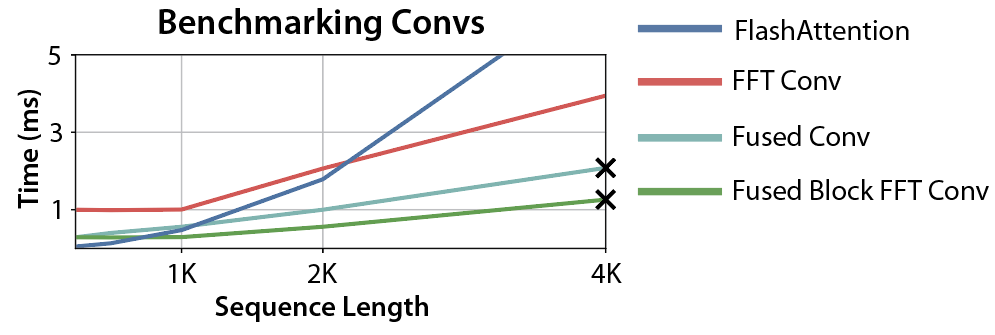
More progress! Now the convolution is faster than FlashAttention for any sequence lengths greater than 512 – which is pretty good!

But what are those X marks?

Beyond SRAM: State-Passing
Let’s return to the original step: fusing the convolution together without writing intermediate results to GPU HBM. This is only possible if all the intermediates can fit into GPU SRAM, which is very small (hundreds of KBs on A100). In our case, it means that we can’t fuse operations longer than 4K in sequence length.

But here, the recurrent properties of SSMs save us again! SSMs admit a recurrent view, which lets us stop the convolution halfway through, save a state vector, and restart it. For our purposes, that means that we can split the convolution into chunks, and then sequentially use our block FFT on each chunk – running the state update at every point.

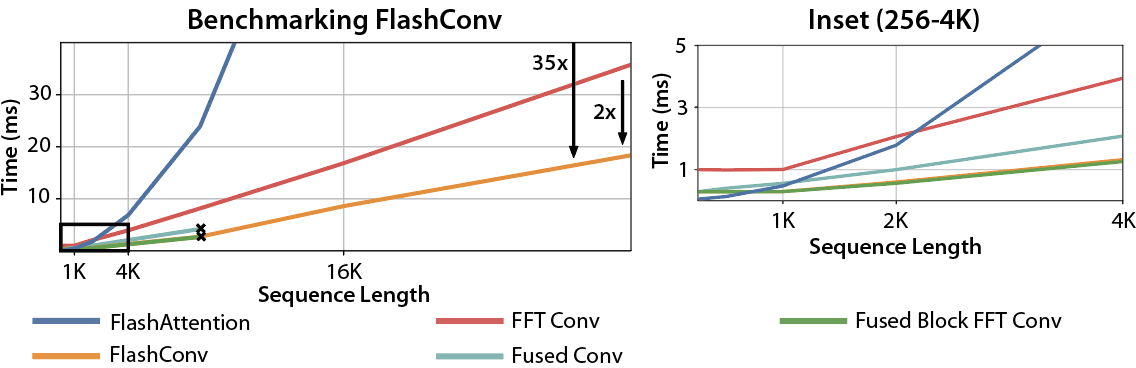
Putting it all together gives us FlashConv, which lets us speed up convolutions by up to 2x over the naive solutions, and outperforms FlashAttention by up to 35x at long sequence lengths.

Fast Training

We can use FlashConv to speed up model training. On the LRA benchmark, we see up to 5.8x speedup over Transformers:

Transformer: 1x
FlashAttention: 2.4x
S4: 2.9x
S4 + FlashConv: 5.8x

We used this speedup to replace attention with SSMs in language models, and scaled our approaches up to 2.7B parameters. Check out our blog post on Hazy Research for more details on H3, the new architecture we developed to get there!

Fast Inference

We compare the generation throughput of a hybrid H3 model and a Transformer model at 1.3B size. For batch size 64, with prompt length 512, 1024, and 1536, hybrid H3 is up to 2.4x faster than Transformer in inference:

Check out our blog post on Hazy Research for more details on H3, the new architecture we developed to get there!

What’s Next

We’re very excited about developing new systems innovations that allow new ideas in deep learning to flourish. FlashConv was critical to the development and testing of H3, a new language modeling approach that uses almost no attention layers.

We’re super excited by these results, so now we’re releasing our code and models to the public! Our code and models are all available on GitHub. If you give it a try, we’d love to hear your feedback!